| Introduction : | ||
|
Trouver une solution à un tableau donné du jeu Sokoban n'est pas toujours chose
facile (c'est d'ailleurs le but du jeu), mais même lorsque vous l'aurrez trouvée,
vous pourrez encore passer de nombreuses heures sur ce même tableau en cherchant
à améliorer votre solution. Mais qu'entend-t-on par améliorer une solution ? La plupart des programmes du jeu Sokoban fournissent des indicateurs pour vos solutions. Les plus courants sont le nombre de mouvements ainsi que le nombre de poussées. J'ai aussi défini deux autres indicateurs qui sont le nombre de poussées en ligne et surtout le nombre de changements de caisse. Sebastien Gouezel est à l'origine d'un autre indicateur : le nombre de phases de rangement. Améliorer une solution consiste simplement à réduire la valeur donnée par tel ou tel indicateur. Comme nous le vérons plus loin il n'est pas toujours possible d'améliorer simultanément la valeur de plusieurs indicateurs, mais avant d'aller plus loin, commençons par définir ces cinq indicateurs : |
||
| Le nombre de mouvements : | ||
|
Cet indicateur est le plus simple. Il représente tout simplement le nombre de déplacements
effectuées par le magasinier pour ranger toutes les caisses. Certains programmes tels que Winsoko où mon propre player anule le dernier mouvement lorsque le magasinier revient sur ses pas d'autres tels que SokoMind comptablisent ces mouvements. Pour évaluer le nombre de mouvements à partir d'un LuRd, il suffit de prendre la longueur du LuRd. |
||
| Le nombre de poussées : | ||
|
Le nombre de poussées d'une solution est le nombre de fois que le magasinier à poussée une caisse.
Il est évident que ce nombre est inférieur ou égal à celui du nombre de mouvements ! Pour évaluer le nombre de poussées à partir d'un LuRd, il suffit de compter le nombre de lettres majuscules présentes dans le LuRd. |
||
| Le nombre de poussées en ligne : | ||
|
Le nombre de poussées en ligne se calcule de la fa çon suivante : une poussée en ligne
correspond à la poussée d'une caisse par le magasinier dans une direction donnée. Le
nombre de cases sur laquelle la caisse a été poussée n'est pas considéré. Ainsi, si le magasinier
pousse une caisse de 1, de 3 ou même de 25 cases vers la gauche, cela n'est comptabilisé
que comme une unique poussée en ligne. Il est ici aussi évident que le nombre de poussées en ligne est inférieur ou égal au nombre de poussées. Remarque: Bien que l'idée de compter les poussées en ligne me soit venue pendant mes propres réflexions, j'ai découvert que certains y avaient déjà songé : dans l'article de Yoshio Murase, Hitoshi Matsubara & Yuzuru Hiraga intitulé "Automatic Making of Sokoban Problems" il est fait référence dans le paragraphe traitant de l'évalution des puzzle généré de ce que j'appelle les poussées en ligne : the number of changes in directions of pushing in solution sequence: in interesting problems the keeper has to change the directions of pushing objects very often. |
||
| Le nombre de changements de caisse : | ||
|
Un changement de caisse est compté à chaque fois que le magasinier cesse de s'occuper d'une caisse
pour une autre. Autrement dit, tant que le magasinier pousse la même caisse, il n'y a pas de changement
comptabilisé. Mais il suffit qu'il pousse une seule fois une autre caisse pour qu'un changement soit
compté. Au tout début du tableau, il n'y a bien sûr aucun changement de caisse, mais la toute première
poussée coïncidera avec le premier changement de caisse. Un petit peu de réflexion vous permettra de constater que le nombre de changements de caisse est toujours inférieur ou égal au nombre de poussées en ligne. Le nombre de changements de caisse est une idée de mon cru. Je n'ai à ce jour trouvé mention nulle part. J'ai pensé à cet indicateur car il me semblait qu'il correspondait le mieux à la façon de raisonner des gens (en tout cas il correspond à ma façon de réfléchir lorsque je résouds des problèmes sokobanesques). Depuis cet indicateur a gagné d'avantage encore en intéret. Effectivement, de plus en plus de programmes proposent une fonction permettant de sélectionner une caisse et d'indiquer la case où on désire que le magasinier la range (le programme se chargeant de trouver le meilleur chemin). Il est clair que les indicateurs de mouvement ou de poussées n'ont plus grand intéret dés qu'on utilise ce type de fonctionnalités tandis que le nombre de changements de caisses correspond précisément à cette façon de jouer ! Evaluer le nombre de changements de caisse à partir d'un LuRd nécissite un peu de travail. Je n'ai pas trouvé de façon de l'évaluer sans simuler l'exécution de la solution et d'analyser les déplacements du magasinier. A expliquer... |
||
| Le nombre de phases de rangement : | ||
|
Le nombre de phases de rangement d'une solution est le nombre de séries de poussées qu'effectuent
le magasinier. Les séries de poussées sont séparées par un déplacement du magasinier. Cet indicateur est particulier car pour optimiser une solution par rapport à cette valeur, il faut complètement modifier sa façon de résoudre le tableau : on doit trouver un équilibre entre des étapes de regroupement des caisses et des étapes de rangements de plusieur caisses d'un coup. Le nombre de phases de rangement est toujours inférieur ou égal à celui des poussées en ligne (une phase de rangement peut se composer de plusieur poussées en ligne). Par contre il n'y a pas de règle générale pour ce qui est de comparer cette valeur avec le nombre de changements de caisse : il est clair que pour tout tableau n'ayant qu'une seule caisse, ce nombre est supérieur au nombre de changement de caisse (qui dans ces cas vaut toujours 1). Par contre, pour tout les tableaux de la famille de George Meier (voir plus loin), le nombre de changements de caisse est égal au nombre de caisses tandis que le nombre de phases de rangement est égal à 1. Pour évaluer le nombre de phases de rangement à partir d'un LuRd, il suffit de compter le nombre de suites de lettres majuscules présentes dans le LuRd. |
||
| Optimiser simultanément plusieur indicateurs : | ||
|
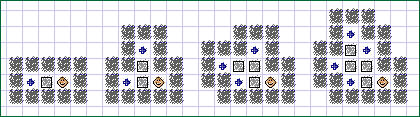
Il est généralement assez difficile de trouver une solution optimale pour un indicateur donné,
mais il est bien plus difficile encore de trouver une solution optimale pour plusieurs indicateurs
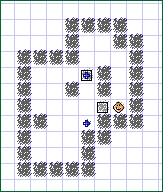
simultanément. Cela s'avère même être impossible dans la plupart des cas ! C'est pourquoi la famille de tableau que m'a suggérée George Meier et qui est présentée ci-dessous est particulière : Effectivement, pour cette famille de tableaux, non seulement il existe une solution optimisant simultanément les cinq indicateurs (saurez-vous la trouver ;) ?), mais en plus la valeur des quatres premiers indicateurs est la même et le nombre de phases de rangement est de 1. Pour la majorité des tableaux, il est impossible d'obtenir des valeurs optimales pour les cinq indicateurs avec une seule solution. J'ai créé le tableau ci-dessous pour montrer cette impossibilité : Les valeurs minimales des indicateurs sont 21 mouvements, 6 poussées, 4 poussées en ligne, 1 changement de caisse et 4 phases de rangement ! Je vous laisse trouver les solutions correspondantes et je dis bien les car il est impossible d'atteindre deux des quatres premières valeurs avec une même solution ! Ce puzzle occupe 29 cases et contient 2 caisses. Il est évident qu'il est impossible d'avoir un tableau présentant cette particularité avec moins de caisses (toutes les solutions d'un tableau qui n'a qu'une caisses n'utilise qu'un seul changement de caisse !). Cependant saurez vous en créer un ayant la même propriété, mais de plus petite taille ? Je vous laisse aussi le soin de trouver un puzzle pour lequel il ne soit pas possible d'atteindre la valeur optimale de deux des cinq indicateurs par la même solution ! Bonne Chance. |
||